Energy in Simple Harmonic Motion

The average power transmitted through a given point on a string supporting a sine wave is. $0.40 \mathrm{W}$ when the amplitude of wave is$2 \mathrm{mm}$. What average power will be transmitted through this point if its amplitude is increased to $4 \mathrm{mm}$

A body of mass $1 \mathrm{kg}$ falls freely from a height of $100 \mathrm{m}$, on a platform of mass $3 \mathrm{kg}$ which is mounted on a spring having spring constant$k=1.25\times {10}^6 \mathrm{N} {\mathrm{m}}^{-1}$. The body sticks to the platform and the spring's maximum compression is found to be$x$. Given that $g=10 \mathrm{m} {\mathrm{s}}^{-2}$, the value of $x$ will be close to 

Total energy of a particle of mass $200 \mathrm{g}$ performing linear SHM is ${10}^{-3} \mathrm{J}$. Find its maximum velocity.

The potential energy of a long spring when stretched by $2 \mathrm{cm}$ is $U$. If the spring is stretched by $8 \mathrm{cm}$, potential energy stored in it will be:

At a given point of time the value of displacement of a simple harmonic oscillator is given as $y=A \cos \left(30°\right).$ If amplitude is $40 \mathrm{cm}$ and kinetic energy at that time is $200 \mathrm{J},$ the value of force constant $1.0\times {10}^x \mathrm{N} {\mathrm{m}}^{–1}$. The value of $x$ is _____.

A particle executes SHM of amplitude$A$. The distance from the mean position when its kinetic energy becomes equal to its potential energy is:

A particle is executing simple harmonic motion (SHM). The ratio of potential energy and kinetic energy of the particle when its displacement is half of its amplitude will be

Which graph represents the difference between total energy and potential energy of a particle executing $\mathrm{SHM}$ vs its distance from mean position?

The variation of kinetic energy (KE) of a particle executing simple harmonic motion with the displacement ($x$) starting from mean position to extreme position ($A$) is given by

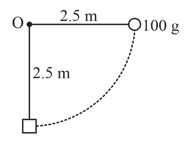
The $100 \mathrm{g}$ bob of a pendulum, left free from horizontal position strikes a $200 \mathrm{g}$ block placed at rest directly below the point of suspension $O$. If the bob comes to rest, find the velocity gained by block just after collision.

A particle is performing S.H.M whose distance from mean position varies as $x=A\sin \left(\omega t\right)$. Find the position of particle from mean position, where kinetic energy and potential energy is equal.

A particle is performing SHM having position $x=A\cos 30°$ and $A=40 \mathrm{cm}$. If its kinetic energy at this position is $200 \mathrm{J}$, the value of force constant in $\left(\frac{\mathrm{kN}}{\mathrm{m}}\right)$  is

The maximum kinetic energy of a mass of $1 \mathrm{kg}$ executing SHM is $18$ Joules. The amplitude of motion is $6$ centimeter. Its angular frequency is

Work done to elongate a spring by $x$from natural length is$w$. Which of the following is correct?
 

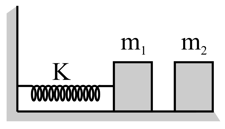
Masses $m_1$and $m_2$ and a spring whose spring constant is $K$are arranged according to the following figure. If the masses$m_1$ and $m_2$ are displaced towards left so that they compress the spring through a distance $d$, the amplitude of oscillation of mass when the spring system is made free, will be-

When a body of mass m is suspended from a spiral spring of natural length$L$, the spring gets stretched through a distance $h$. The potential energy of the stretched spring is

A particle is undergoing SHM, when its kinetic energy is equal to potential energy, the velocity of particle is ( $\omega$ angular frequency, $A$ - amplitude and potential energy at mean position is zero)
 

A particle is executing SHM. At a point $x=\frac{A}{3}$, kinetic energy of the particle is $K$, where $A$is the amplitude. At a point $x=\frac{2A}{3}$, kinetic energy of the particle will be:

A particle is undergoing SHM, when its kinetic energy is equal to potential energy, the velocity of particle is ($\omega$- angular frequency,$A$- amplitude and potential energy at mean position is zero)
 

A spring of force constant$k$is cut in two parts at its one third length. When both the parts are stretched by same amount, the work done in the two parts, will be
(1) equal in both
(2) greater for the longer part
(3) greater for the shorter part
(4) data insufficient